Definition and Scope of Mathematical Physics
Mathematical physics is the rigorous application of advanced mathematical frameworks to describe and analyze physical phenomena. It serves as the bridge between abstract mathematical concepts and their practical implications in understanding the natural world. The field relies heavily on tools like differential equations, linear algebra, and calculus of variations to model and solve physical problems. By integrating these mathematical tools, physicists can formulate theories, predict outcomes, and validate experimental results. This interdisciplinary approach ensures precision and consistency in explaining complex systems, from classical mechanics to quantum theory. Resources such as Mathematical Methods for Physicists by Arfken and online PDF notes provide detailed insights into these mathematical foundations.
The Role of Mathematics in Physics
Mathematics is the fundamental language of physics, enabling precise descriptions of physical phenomena and the formulation of universal laws. It provides the tools to model complex systems, from classical mechanics to quantum mechanics. Equations, such as differential equations and tensor calculus, are central to theoretical physics, offering a framework for predicting and analyzing experimental results. Mathematics ensures logical consistency and rigor, allowing physicists to understand and validate their theories. As emphasized in resources like Mathematical Methods for Physicists and various PDF notes, the interplay between mathematics and physics is essential for advancing our understanding of the natural world. Mathematics not only describes physics but also shapes its identity and progress.
Historical Development of Mathematical Physics
Mathematical physics has evolved significantly since its inception, with key contributions from pioneers like Newton, Maxwell, and Einstein. Newton’s laws of motion and universal gravitation laid the groundwork, while Maxwell unified electricity and magnetism through equations. The 20th century saw quantum mechanics emerge, with Schrödinger and Heisenberg introducing wave mechanics and matrix mechanics. Einstein’s theory of relativity revolutionized spacetime concepts; Historical resources, such as textbooks by Courant and Hilbert, highlight the development of mathematical tools like differential equations and tensor calculus. These advancements demonstrate how mathematics has historically shaped physics, providing frameworks for understanding natural phenomena. The interplay between mathematical rigor and physical intuition has driven progress, as documented in various PDF notes and classical texts.
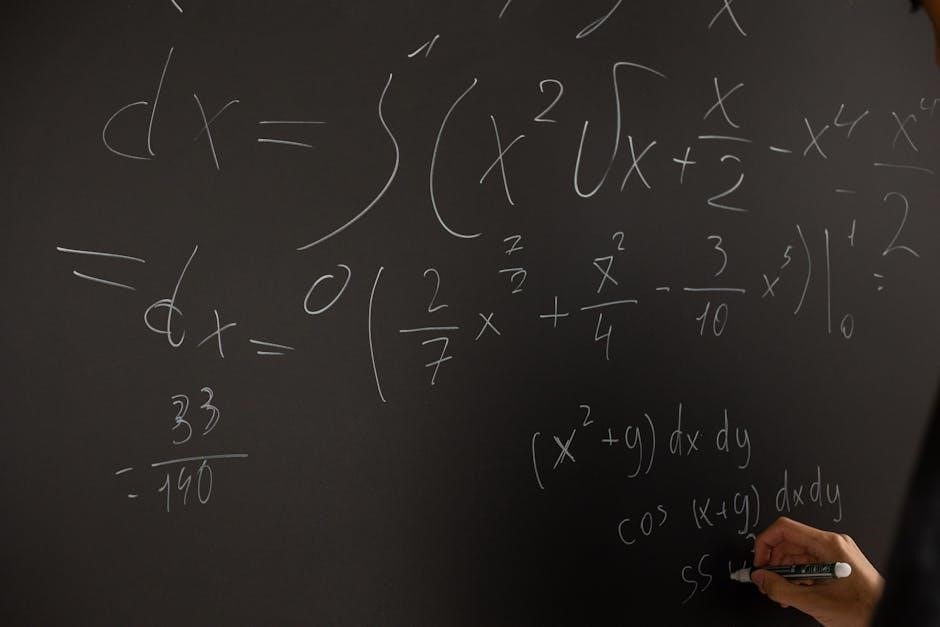
Core Mathematical Tools in Physics
Core mathematical tools in physics, such as differential equations, linear algebra, and Fourier transforms, are essential for modeling and analyzing physical systems, as detailed in resources like Arfken’s and Hassani’s textbooks.
Differential Equations in Physics
Differential equations are fundamental in physics, describing how physical quantities change over space and time. They are central to modeling phenomena like motion, heat transfer, and wave propagation. These equations often arise from physical laws, such as Newton’s laws or Maxwell’s equations. Solving them provides insights into system behavior, enabling predictions and analyses. Resources like Arfken’s Mathematical Methods for Physicists and Hassani’s Mathematical Physics offer detailed treatments of differential equations, emphasizing their role in classical mechanics, electromagnetism, and quantum mechanics. PDF lecture notes and textbooks also highlight their importance, showcasing applications in various fields and providing step-by-step solutions to complex problems. These tools are indispensable for both undergraduates and researchers in mathematical physics.
Linear Algebra and Its Applications
Linear algebra is a cornerstone of mathematical physics, providing tools to describe vector spaces, matrices, and linear transformations. It is essential for understanding quantum mechanics, where Hilbert spaces and operators are fundamental. Applications include solving systems of differential equations, analyzing symmetry in physical systems, and simplifying complex problems through eigenvalue decomposition. Resources like Mathematical Methods for Physicists by Arfken and online PDF notes detail its role in physics, offering practical examples and proofs. Linear algebra also underpins relativity, particularly in tensor analysis, and is crucial for computational physics. Its versatility makes it a foundational area, with textbooks and lecture notes providing comprehensive guidance for students and researchers alike.
Calculus of Variations and Optimization
The calculus of variations is a mathematical discipline focused on optimizing functionals, which are mappings from functions to real numbers. It is central to theoretical physics, particularly in the formulation of Lagrangian and Hamiltonian mechanics. By minimizing action integrals, physicists derive equations of motion, fundamental to both classical and quantum systems. Optimization techniques from this field are also applied in statistical mechanics and relativistic theories. Resources such as graduate-level PDF notes and textbooks like Mathematical Physics by Sadri Hassani provide detailed explanations, including examples and proofs, to illustrate its applications. These tools are essential for understanding the mathematical underpinnings of physical laws and developing predictive models in various fields of physics.
Fourier Transforms and Their Significance
Fourier transforms are a cornerstone of mathematical physics, enabling the decomposition of complex functions into their constituent frequencies. This tool is indispensable for solving partial differential equations, analyzing wave phenomena, and simplifying complex systems. In quantum mechanics, Fourier transforms connect position and momentum spaces, while in signal processing, they facilitate frequency analysis. PDF resources and textbooks, such as Arfken’s Mathematical Methods for Physicists, provide detailed explanations and applications, illustrating their role in physics. Fourier transforms are essential for understanding oscillatory behavior, diffusive processes, and electromagnetic waves. Their ability to transform problems between time and frequency domains makes them a fundamental technique in theoretical and applied physics, bridging mathematics and physical intuition.
Applications of Mathematical Physics
Classical Mechanics and Its Mathematical Foundations
Classical mechanics, a cornerstone of physics, relies heavily on mathematical frameworks to describe motion and forces. Differential equations, derived from Newton’s laws, form the basis for analyzing dynamical systems. PDF resources and textbooks, such as those by Sadri Hassani, provide detailed explanations of these mathematical foundations. Topics include Lagrangian mechanics, Hamiltonian formulations, and the role of symmetry in conservation laws. These tools are essential for solving problems in both theoretical and applied physics, offering a rigorous approach to understanding classical systems. The integration of linear algebra and calculus further enhances the analytical power of classical mechanics, making it a fundamental area of study in mathematical physics.
Quantum Mechanics and Hilbert Spaces
Quantum mechanics is deeply rooted in the mathematical framework of Hilbert spaces, where state vectors and operators describe physical systems. These spaces provide the foundation for wave functions, probability amplitudes, and observables. PDF resources, such as lecture notes from King’s College London, detail the role of spectral theory and operator algebra in quantum systems. The mathematical rigor of Hilbert spaces ensures precise formulations of quantum principles, enabling the solution of Schrödinger equations and the analysis of quantum states. Textbooks like Sadri Hassani’s Mathematical Physics offer comprehensive coverage of these concepts, making them indispensable for advanced studies in theoretical physics.
Relativity and Tensor Calculus
Tensor calculus is a cornerstone of Einstein’s theory of relativity, both special and general. It provides the mathematical framework for describing spacetime and gravity. In general relativity, tensors are used to express the curvature of spacetime caused by mass and energy. PDF resources, such as lecture notes from King’s College London, detail the application of tensor analysis in relativistic physics. Key concepts include the metric tensor, Christoffel symbols, and the Einstein field equations. These tools enable physicists to solve complex problems in cosmology and gravitational physics. Textbooks like Sadri Hassani’s Mathematical Physics offer in-depth discussions of tensor operations and their role in modern relativistic theories, making them essential for advanced studies in theoretical physics;
Statistical Mechanics and Probability Theory
Statistical mechanics, a bridge between thermodynamics and molecular theories, relies heavily on probability theory and mathematical physics. PDF resources, such as lecture notes from various universities, explore the foundational principles of statistical distributions and their applications in understanding systems at microscopic scales. Key concepts include Boltzmann distributions, entropy, and the use of partition functions to describe equilibrium states. Probability theory is integral in analyzing stochastic processes and fluctuations in physical systems. Textbooks like Mathematical Physics by Sadri Hassani provide detailed derivations of statistical mechanics frameworks, linking them to experimental observations. These mathematical tools are essential for studying phase transitions, quantum statistics, and the behavior of matter under varying conditions, making them a cornerstone of modern theoretical physics research and education.

Notable Textbooks and Resources
Key textbooks include Mathematical Methods for Physicists by Arfken and Mathematical Physics by Hassani, offering comprehensive coverage of mathematical tools and their applications in physics.
“Mathematical Methods for Physicists” by Arfken
Mathematical Methods for Physicists by George Arfken is a seminal textbook widely used by graduate students in physics and engineering. It provides a comprehensive treatment of mathematical techniques essential for solving physical problems, including differential equations, linear algebra, and special functions. The book is known for its clear explanations and practical examples, making advanced mathematical concepts accessible to students with varying levels of mathematical sophistication. It covers topics such as vector analysis, complex variables, and group theory, with applications in classical mechanics, electromagnetism, and quantum mechanics. Arfken’s text is structured to build a strong foundation, ensuring students can apply these methods to cutting-edge research and problem-solving in physics.
“Mathematical Physics” by Sadri Hassani
Mathematical Physics by Sadri Hassani is a modern introduction to the field, designed for advanced undergraduate and graduate students. It integrates mathematical rigor with physical intuition, covering essential topics such as differential equations, Fourier transforms, and special functions. The text emphasizes the interplay between mathematics and physics, providing clear proofs and practical examples. Hassani’s approach ensures that students understand both the mathematical derivations and their physical interpretations. The book also includes discussions on emerging trends and applications, making it a valuable resource for those pursuing theoretical and applied physics. Its comprehensive coverage and accessible style have made it a popular choice among students and educators alike.
Online Lecture Notes and PDF Resources
Various online resources provide comprehensive lecture notes and PDFs on mathematical physics, catering to both undergraduate and graduate levels. Websites like Cambridge University and King’s College London offer detailed notes on topics such as classical mechanics, quantum mechanics, and tensor calculus. These resources often include explanations of key mathematical tools, like Fourier transforms and differential equations, with practical examples. Additionally, PDF documents on platforms like Zhihu and academic repositories cover special functions, integral equations, and operator theory. Many of these materials are designed for self-study, offering clear proofs and applications. They serve as invaluable supplements to textbooks, providing accessible learning opportunities for students and researchers in mathematical physics.
Special Functions in Mathematical Physics
Special functions like Bessel functions and Legendre polynomials are essential in solving physical problems, appearing in wave equations and potential theory, with detailed PDF resources available online.
Bessel Functions and Their Applications
Bessel functions are canonical solutions to Bessel’s differential equation, arising in problems with cylindrical symmetry, such as wave propagation and heat transfer; They are classified into types like BesselJ and BesselY, each with specific properties; These functions are widely used in physics and engineering, particularly in acoustics, electromagnetism, and quantum mechanics. For instance, they describe the vibrations of circular membranes and the modes of electromagnetic waves in waveguides. A comprehensive PDF resource on special functions in mathematical physics details their definitions, series expansions, and applications, providing solutions to differential equations involving Bessel functions. Their importance is underscored by their ability to model real-world phenomena accurately, making them indispensable in theoretical and applied physics.
Legendre Polynomials and Spherical Harmonics
Legendre polynomials are orthogonal polynomials on the interval [-1, 1], while spherical harmonics extend these concepts to the sphere. Both are pivotal in solving partial differential equations with spherical symmetry, such as the Laplace equation. Legendre polynomials arise in problems involving azimuthal symmetry, while spherical harmonics incorporate both polar and azimuthal angles, forming a complete orthonormal basis. Their orthogonality simplifies solutions in physics, particularly in quantum mechanics for angular momentum and in geophysical models. A detailed PDF resource explains their properties, including generating functions and recursion relations, and their applications in wave equations and potential theory, making them essential tools in theoretical physics and engineering.
Elliptic Functions and Their Role
Elliptic functions, introduced by Jacobi, are doubly periodic meromorphic functions with profound applications in physics. They arise in solving certain nonlinear differential equations, such as the pendulum equation, and are integral to lattice vibration studies and gravitational potential calculations. These functions extend trigonometric functions to elliptic cases, offering a mathematical framework for periodic phenomena. In physics, they model wave propagation in crystals and electron dynamics in solids. Their properties, like modular symmetry, connect them to quantum mechanics and string theory. A comprehensive PDF resource details their historical development, mathematical properties, and physical applications, serving as a bridge between pure mathematics and physical phenomena, essential for advanced theoretical modeling and computational methods in modern physics.

Modern Advances in Mathematical Physics
Modern advances in mathematical physics involve group theory for symmetry analysis, functional analysis for operator theories, and computational methods for complex simulations, driving emerging trends in the field.
Group Theory and Symmetry in Physics
Group theory is a fundamental area of mathematics that studies symmetry, crucial in physics for understanding transformations and invariance. Symmetry plays a central role in quantum mechanics, particle physics, and relativity. Group representations classify particles and interactions, aiding in the formulation of quantum field theories. Lie groups, such as SU(2) and SU(3), are essential for describing gauge symmetries in the Standard Model. PDF resources and textbooks detail these applications, emphasizing how group theory provides a mathematical framework for symmetry principles. This framework underpins conservation laws and the behavior of physical systems, making it a cornerstone of modern theoretical physics.
Functional Analysis and Operator Theory
Functional analysis and operator theory are pivotal in mathematical physics, particularly in quantum mechanics and relativity. These fields deal with infinite-dimensional vector spaces and linear operators, essential for describing physical systems. Hilbert spaces, a cornerstone of quantum mechanics, rely on operator theory to represent observables and states. The spectral theorem and operator algebras provide tools for analyzing the behavior of physical systems. PDF resources and textbooks, such as those by Sadri Hassani, emphasize the role of functional analysis in solving differential equations and understanding operator spectra. This mathematical framework is crucial for advancing theoretical physics, enabling precise descriptions of complex phenomena and the formulation of new theories.
Computational Methods in Physics
Computational methods in physics involve numerical simulations and algorithms to solve complex mathematical models. These techniques are essential for analyzing systems that cannot be easily solved analytically. Numerical methods, such as finite difference and finite element approaches, are widely used in fluid dynamics, quantum mechanics, and relativity. Computational tools like MATLAB and Python libraries enable physicists to simulate experiments, visualize data, and predict outcomes. PDF resources and textbooks often include computational techniques, emphasizing their role in modern research. These methods bridge theory and experimentation, accelerating discoveries in areas like climate modeling, materials science, and particle physics. Computational physics has become indispensable, offering precise solutions to intricate problems and driving advancements in theoretical and applied physics.
The Interplay Between Mathematics and Physics
Mathematics serves as the foundational language of physics, enabling the precise description and analysis of natural phenomena. Equations and frameworks derived from mathematical principles form the cornerstone of theoretical physics. The interplay between the two disciplines fosters advancements in both fields, with mathematics providing the tools to model physical systems and physics inspiring new mathematical theories. This symbiotic relationship is evident in the development of differential equations, linear algebra, and calculus, which are pivotal in understanding mechanics, electromagnetism, and quantum theory. By leveraging mathematical rigor, physicists can explore complex phenomena, while mathematicians often find motivation in the practical challenges posed by physics. This interplay continues to drive innovation, ensuring that both fields remain deeply intertwined in their pursuit of knowledge.
Emerging Trends in Mathematical Physics
Mathematical physics continues to evolve, driven by advancements in computational methods and interdisciplinary approaches. Emerging trends include the integration of artificial intelligence and machine learning to solve complex physical problems, enabling faster and more accurate simulations. There is also a growing focus on quantum information theory, where mathematical frameworks are developed to understand and control quantum systems. Additionally, the application of advanced mathematical tools, such as topology and category theory, is opening new avenues in condensed matter physics and theoretical physics. These trends highlight the dynamic interplay between mathematical innovation and physical discovery, paving the way for breakthroughs in fields like quantum computing, biophysics, and cosmology.