Continuous function pdf Bay of Plenty
CONTINUITY 26 3. Continuous Functions Example 3.17. The function f: R в†’ R given by f(x) = x+3x3 +5x5 1+x2 +x4 is continuous on R since it is a rational function whose denominator never vanishes. In addition to forming sums, products and quotients, another way to build up
Continuity (exercises with detailed solutions)
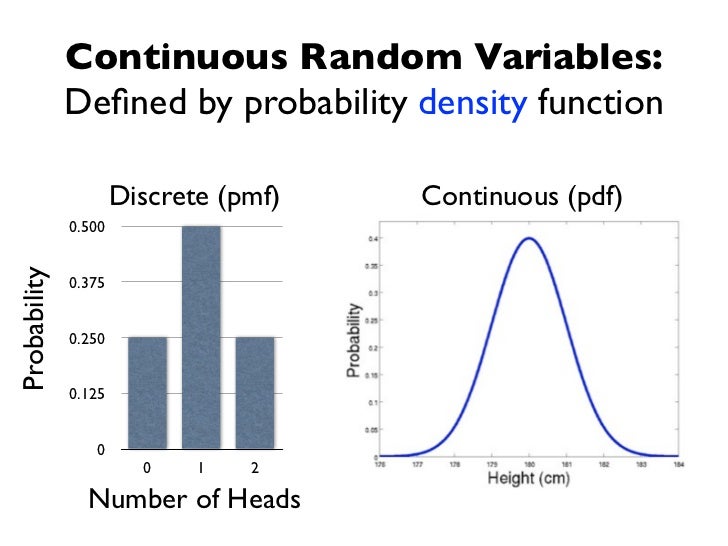
Continuous Functions. C. CONTINUITY AND DISCONTINUITY 3 We say a function is continuous if its domain is an interval, and it is continuous at every point of that interval. A point of discontinuity is always understood to be isolated, i.e., it is the only bad point for the function on some interval. We illustrate the point of these definitions., When deflning a distribution for a continuous RV, the PMF approach won’t quite work since summations only work for a flnite or a countably inflnite number of items. Instead they are based on the following Deflnition: Let X be a continuous RV. The Probability Density Function (PDF) is a function f(x) on the range of X that satisfles the.
sum of continuous functions is a continuous function, and that a multiple of a continuous function is a continuous function. For real-valued functions (i.e., if Y = R), we can also de ne the product fg and (if 8x2X: f(x) 6= 0) the reciprocal 1 =f of functions pointwise, and we can show that if f and gare continuous then so are fgand 1=f. 2 described with a joint probability mass function. If Xand Yare continuous, this distribution can be described with a joint probability density function. Example: Plastic covers for CDs (Discrete joint pmf) Measurements for the length and width of a rectangular plastic covers for CDs are rounded to the nearest mm(so they are discrete).
A function f is said to be continuous from the left at a if lim f ( x) = f ( a). x в†’ a в€’ A function f is said to be continuous on an interval if it is continuous at each and every point in the interval. Continuity at an endpoint, if one exists, means f is continuous from the right (for the left endpoint) or continuous At a point where f.x/ has a derivative, the function must be continuous. But f.x/ can be continuous with no derivative. Here are two essential facts about a continuous function on a closed interval a В¤ x b. At the endpoints a and b, we require f.x/ to approach f.a/ and f.b/: 4
The function f(x) = x2 is continuous at x = 0 by this definition. It is also continuous at every other point on the real line by this definition. If a function is continuous at every point in its domain, we call it a continuous function. The following functions are all continuous: 1 †Probability Density Functions De nition Let X be a continuous rv. Then a probability distribution or probability density function (pdf) of X is a function f(x) such that for any two numbers a and b with a b, P(a X b) = Z b a f(x)dx That is, the probability that X takes on a value in the interval [a;b] is the
An Important Subtlety. There is an important subtlety in the definition of the PDF of a continuous random variable. Notice that the PDF of a continuous random variable X can only be defined when the distribution function of X is differentiable.. As a first example, consider the experiment of randomly choosing a real number from the interval [0,1]. The probability density function or PDF of a continuous random variable gives the relative likelihood of any outcome in a continuum occurring. Unlike the case of discrete random variables, for a continuous random variable any single outcome has probability zero of occurring. The probability density function gives the probability that any value in a continuous set of values might occur.
It is obvious that a uniformly continuous function is continuous: if we can nd a which works for all x 0, we can nd one (the same one) which works for any particular x 0. We will see below that there are continuous functions which are not uniformly continuous. Example 5. Let S= R and f(x) = 3x+7. Then fis uniformly continuous on S. Proof Probability Distributions for Continuous Variables Definition Let X be a continuous r.v. Then a probability distribution or probability density function (pdf) of X is a function f (x) such that for any two numbers a and b with a ≤ b, we have The probability that X is in the interval [a, b] can be calculated by integrating the pdf …
For example, at the value x equal to 3, the corresponding pdf value in y is equal to 0.1804. Alternatively, you can compute the same pdf values without creating a probability distribution object. Use the pdf function, and specify a Poisson distribution using the same value for the rate parameter, λ. Continuity (exercises with detailed solutions) 1. Verify that f(x) = p x is continuous at x0 for every x0 ‚ 0. 2. Verify that f(x) = 1 x ¡ 1 x0 is continuous at x0 for every x0 6= 0. 3. Draw the graph and study the discontinuity points of f(x) = [sinx]. 4.
continuous function between tw o comparable real-valued functions. If g and f are re al-valued func tions defined on a space X , we write f g . resp A function f is said to be continuous from the left at a if lim f ( x) = f ( a). x в†’ a в€’ A function f is said to be continuous on an interval if it is continuous at each and every point in the interval. Continuity at an endpoint, if one exists, means f is continuous from the right (for the left endpoint) or continuous
C. CONTINUITY AND DISCONTINUITY 3 We say a function is continuous if its domain is an interval, and it is continuous at every point of that interval. A point of discontinuity is always understood to be isolated, i.e., it is the only bad point for the function on some interval. We illustrate the point of these deп¬Ѓnitions. function is continuous. The following theorem says justthat. Theorem 1 Ifthe function f is differentiable at xo, then f is continuous at Xo. Proof We need to verify that conditions 1 and 2 ofthe definition ofconВ
continuous on R. f is Lipschitz continuous on R; with L = 1: This shows that if A is unbounded, then f can be unbounded and still uniformly continuous. The function x2 is an easy example of a function which is continuous, but not uniformly continuous, on R. If we jump ahead, and assume we know about derivatives, we can see a rela- At a point where f.x/ has a derivative, the function must be continuous. But f.x/ can be continuous with no derivative. Here are two essential facts about a continuous function on a closed interval a В¤ x b. At the endpoints a and b, we require f.x/ to approach f.a/ and f.b/: 4
Determine if a function is continuous on a given interval. A variation of this question is to determine the set (that is all the values of x) on which a function is continuous. Whenever possible, try to use the theorems. But in situations where the theorems do not apply, you must use the de–nition of … For example, at the value x equal to 3, the corresponding pdf value in y is equal to 0.1804. Alternatively, you can compute the same pdf values without creating a probability distribution object. Use the pdf function, and specify a Poisson distribution using the same value for the rate parameter, λ.
Section 4.2 Discrete and Continuous Domains 155 Work with a partner. Write a function to represent each problem. Graph each function. Describe the domain and range of each function. Is the domain discrete or continuous? 2 ACTIVITY: Discrete and Continuous Domains a. You are in charge of reserving continuous function between tw o comparable real-valued functions. If g and f are re al-valued func tions defined on a space X , we write f g . resp
5 Continuity

5 Continuity. described with a joint probability mass function. If Xand Yare continuous, this distribution can be described with a joint probability density function. Example: Plastic covers for CDs (Discrete joint pmf) Measurements for the length and width of a rectangular plastic covers for CDs are rounded to the nearest mm(so they are discrete)., It is obvious that a uniformly continuous function is continuous: if we can nd a which works for all x 0, we can nd one (the same one) which works for any particular x 0. We will see below that there are continuous functions which are not uniformly continuous. Example 5. Let S= R and f(x) = 3x+7. Then fis uniformly continuous on S. Proof.
Continuous function Wikipedia. Continuous Functions Q What does it mean for a function to be continuous at a point? Answer- In mathematics, we have a definition that consists of three concepts that are linked in a special way. Consider the following definition. Definition- Let P=(af, (a))be a point on the curve f. We say a function f is continuous at a point P if and only if the following relationship is satisfied., The function f(x) = x2 is continuous at x = 0 by this definition. It is also continuous at every other point on the real line by this definition. If a function is continuous at every point in its domain, we call it a continuous function. The following functions are all continuous: 1 †.
4.2 Discrete and Continuous Domains

Continuous Functions Brilliant Math & Science Wiki. continuous function between tw o comparable real-valued functions. If g and f are re al-valued func tions defined on a space X , we write f g . resp https://sco.wikipedia.org/wiki/Continuous_function The study of continuous functions is a case in point - by requiring a function to be continuous, we obtain enough information to deduce powerful theorems, such as the In-termediate Value Theorem. However, the de nition of continuity is exible enough that there are a wide, and interesting, variety of continuous functions. Indeed, many func-.

Ticket out the Door – Discrete vs. Continuous You are traveling over winter break on a plane from Austin Intercontinental Airport (AUS) to Los Angeles, California (LAX), describe 3 discrete and 3 continuous data examples you might encounter during your trip: Discrete Examples Continuous Examples 1. 1. 2. 2. 3. 3. The study of continuous functions is a case in point - by requiring a function to be continuous, we obtain enough information to deduce powerful theorems, such as the In-termediate Value Theorem. However, the de nition of continuity is exible enough that there are a wide, and interesting, variety of continuous functions. Indeed, many func-
Continuous Functions Q What does it mean for a function to be continuous at a point? Answer- In mathematics, we have a definition that consists of three concepts that are linked in a special way. Consider the following definition. Definition- Let P=(af, (a))be a point on the curve f. We say a function f is continuous at a point P if and only if the following relationship is satisfied. At a point where f.x/ has a derivative, the function must be continuous. But f.x/ can be continuous with no derivative. Here are two essential facts about a continuous function on a closed interval a В¤ x b. At the endpoints a and b, we require f.x/ to approach f.a/ and f.b/: 4
Section 4.2 Discrete and Continuous Domains 155 Work with a partner. Write a function to represent each problem. Graph each function. Describe the domain and range of each function. Is the domain discrete or continuous? 2 ACTIVITY: Discrete and Continuous Domains a. You are in charge of reserving CONTINUITY 1. CONTINUOUS FUNCTIONS : A function for which a small change in the independent variable causes only a small change and not a sudden jump in the dependent variable are called continuous functions. Naively, we may say that a function is continuous
Lecture 5 : Continuous Functions De nition 1 We say the function fis continuous at a number aif lim x!a f(x) = f(a): (i.e. we can make the value of f(x) as close as we like to f(a) by taking xsu ciently close to a). Example Last day we saw that if f(x) is a polynomial, then fis continuous at afor any real number Such a curve is denoted f(x) and is called a (continuous) probability density function. Now, you might recall that a density histogram is defined so that the area of each rectangle equals the relative frequency of the corresponding class, and the area of the entire histogram equals 1.
Continuous Functions Q What does it mean for a function to be continuous at a point? Answer- In mathematics, we have a definition that consists of three concepts that are linked in a special way. Consider the following definition. Definition- Let P=(af, (a))be a point on the curve f. We say a function f is continuous at a point P if and only if the following relationship is satisfied. ©x H2M071H3q qKYuXt2aA yShoOf8t ywmairhe n 0LwL3CH.O T lA ZlVl s 3rgi sg KhptIsX or 8eYs ie 7r CvDeed u.4 x 3M HaRdvex 3w qiCtah8 HIbn Mf8ilnui dt fe …
The probability density function or PDF of a continuous random variable gives the relative likelihood of any outcome in a continuum occurring. Unlike the case of discrete random variables, for a continuous random variable any single outcome has probability zero of occurring. The probability density function gives the probability that any value in a continuous set of values might occur. described with a joint probability mass function. If Xand Yare continuous, this distribution can be described with a joint probability density function. Example: Plastic covers for CDs (Discrete joint pmf) Measurements for the length and width of a rectangular plastic covers for CDs are rounded to the nearest mm(so they are discrete).
Instead, we can usually define the probability density function (PDF). The PDF is the density of probability rather than the probability mass. The concept is very similar to mass density in physics: its unit is probability per unit length. Fig.4.2 - PDF for a continuous … In calculus, a continuous function is a real-valued function whose graph does not have any breaks or holes. Continuity lays the foundational groundwork for the intermediate value theorem and extreme value theorem. They are in some sense the ``nicest" functions possible, and many proofs in real analysis rely on approximating arbitrary functions by continuous functions.
Lecture 5 : Continuous Functions De nition 1 We say the function fis continuous at a number aif lim x!a f(x) = f(a): (i.e. we can make the value of f(x) as close as we like to f(a) by taking xsu ciently close to a). Example Last day we saw that if f(x) is a polynomial, then fis continuous at afor any real number sum of continuous functions is a continuous function, and that a multiple of a continuous function is a continuous function. For real-valued functions (i.e., if Y = R), we can also de ne the product fg and (if 8x2X: f(x) 6= 0) the reciprocal 1 =f of functions pointwise, and we can show that if f and gare continuous then so are fgand 1=f. 2
Probability Distributions for Continuous Variables Definition Let X be a continuous r.v. Then a probability distribution or probability density function (pdf) of X is a function f (x) such that for any two numbers a and b with a ≤ b, we have The probability that X is in the interval [a, b] can be calculated by integrating the pdf … Lecture 17 - Piecewise continuous functions and improper integrals In this lecture, we will review piecewise continuous functions and improper integrals. We will need both of these notions in the next topic: the Laplace Transform. Intuitively, a function is said to be continuous if its graph has no breaks; it can be sketched without without
26 3. Continuous Functions Example 3.17. The function f: R в†’ R given by f(x) = x+3x3 +5x5 1+x2 +x4 is continuous on R since it is a rational function whose denominator never vanishes. In addition to forming sums, products and quotients, another way to build up 26 3. Continuous Functions Example 3.17. The function f: R в†’ R given by f(x) = x+3x3 +5x5 1+x2 +x4 is continuous on R since it is a rational function whose denominator never vanishes. In addition to forming sums, products and quotients, another way to build up
The probability density function or PDF of a continuous random variable gives the relative likelihood of any outcome in a continuum occurring. Unlike the case of discrete random variables, for a continuous random variable any single outcome has probability zero of occurring. The probability density function gives the probability that any value in a continuous set of values might occur. Probability Density Functions De nition Let X be a continuous rv. Then a probability distribution or probability density function (pdf) of X is a function f(x) such that for any two numbers a and b with a b, P(a X b) = Z b a f(x)dx That is, the probability that X takes on a value in the interval [a;b] is the
Continuous Random Variables

Probability Density Functions STAT 414 / 415. CONTINUITY 1. CONTINUOUS FUNCTIONS : A function for which a small change in the independent variable causes only a small change and not a sudden jump in the dependent variable are called continuous functions. Naively, we may say that a function is continuous, Probability Distributions for Continuous Variables Definition Let X be a continuous r.v. Then a probability distribution or probability density function (pdf) of X is a function f (x) such that for any two numbers a and b with a ≤ b, we have The probability that X is in the interval [a, b] can be calculated by integrating the pdf ….
CONTINUITY AND DIFFERENTIABILITY
Discrete vs. Continuous. 26 3. Continuous Functions Example 3.17. The function f: R → R given by f(x) = x+3x3 +5x5 1+x2 +x4 is continuous on R since it is a rational function whose denominator never vanishes. In addition to forming sums, products and quotients, another way to build up, ©x H2M071H3q qKYuXt2aA yShoOf8t ywmairhe n 0LwL3CH.O T lA ZlVl s 3rgi sg KhptIsX or 8eYs ie 7r CvDeed u.4 x 3M HaRdvex 3w qiCtah8 HIbn Mf8ilnui dt fe ….
C. CONTINUITY AND DISCONTINUITY 3 We say a function is continuous if its domain is an interval, and it is continuous at every point of that interval. A point of discontinuity is always understood to be isolated, i.e., it is the only bad point for the function on some interval. We illustrate the point of these definitions. function cannot be continuous at that point. Continuity at a point is a point-wise definition, which we would like to extend to the entire domain of the function. Definition: Continuity A function f is continuous if it is continuous at every point in its domain.
An Important Subtlety. There is an important subtlety in the definition of the PDF of a continuous random variable. Notice that the PDF of a continuous random variable X can only be defined when the distribution function of X is differentiable.. As a first example, consider the experiment of randomly choosing a real number from the interval [0,1]. At a point where f.x/ has a derivative, the function must be continuous. But f.x/ can be continuous with no derivative. Here are two essential facts about a continuous function on a closed interval a В¤ x b. At the endpoints a and b, we require f.x/ to approach f.a/ and f.b/: 4
continuous by appropriately defining (or redefining) For instance, the function in Example 2(b) has a removable discontinuity at To remove the discontinuity, all you need to do is redefine the function so that A discontinuity at is nonremovable if the function cannot be made continuous at by defining or redefining the function at For instance, Discrete Probability Density Function The discrete probability density function (PDF) of a discrete random variable X can be represented in a table, graph, or formula, and provides the probabilities Pr(X = x) for all possible values of x.
26 3. Continuous Functions Example 3.17. The function f: R → R given by f(x) = x+3x3 +5x5 1+x2 +x4 is continuous on R since it is a rational function whose denominator never vanishes. In addition to forming sums, products and quotients, another way to build up Determine if a function is continuous on a given interval. A variation of this question is to determine the set (that is all the values of x) on which a function is continuous. Whenever possible, try to use the theorems. But in situations where the theorems do not apply, you must use the de–nition of …
3.2 Limits and Continuity of Functions of Two or More Variables. 3.2.1 Elementary Notions of Limits We wish to extend the notion of limits studied in Calculus I. Recall that when we write lim x!a f(x) = L, we mean that f can be made as close as we want to L, by taking xclose enough to … continuous by appropriately defining (or redefining) For instance, the function in Example 2(b) has a removable discontinuity at To remove the discontinuity, all you need to do is redefine the function so that A discontinuity at is nonremovable if the function cannot be made continuous at by defining or redefining the function at For instance,
the sinc-function becomes a continuous function on all real numbers. The term removable singularity is used in such cases, when (re)defining values of a function to coincide with the appropriate limits make a function continuous at specific points. A more involved construction of continuous functions is the function composition. Given two continuous function between tw o comparable real-valued functions. If g and f are re al-valued func tions defined on a space X , we write f g . resp
Determine if a function is continuous on a given interval. A variation of this question is to determine the set (that is all the values of x) on which a function is continuous. Whenever possible, try to use the theorems. But in situations where the theorems do not apply, you must use the de–nition of … At a point where f.x/ has a derivative, the function must be continuous. But f.x/ can be continuous with no derivative. Here are two essential facts about a continuous function on a closed interval a ¤ x b. At the endpoints a and b, we require f.x/ to approach f.a/ and f.b/: 4
Such a curve is denoted f(x) and is called a (continuous) probability density function. Now, you might recall that a density histogram is defined so that the area of each rectangle equals the relative frequency of the corresponding class, and the area of the entire histogram equals 1. Instead, we can usually define the probability density function (PDF). The PDF is the density of probability rather than the probability mass. The concept is very similar to mass density in physics: its unit is probability per unit length. Fig.4.2 - PDF for a continuous …
C. CONTINUITY AND DISCONTINUITY 3 We say a function is continuous if its domain is an interval, and it is continuous at every point of that interval. A point of discontinuity is always understood to be isolated, i.e., it is the only bad point for the function on some interval. We illustrate the point of these definitions. An Important Subtlety. There is an important subtlety in the definition of the PDF of a continuous random variable. Notice that the PDF of a continuous random variable X can only be defined when the distribution function of X is differentiable.. As a first example, consider the experiment of randomly choosing a real number from the interval [0,1].
And so for a function to be continuous at x = c, the limit must exist as x approaches c, that is, the left- and right-hand limits -- those numbers -- must be equal. (Definition 2.2) If a function is continuous at every value in an interval, then we say that the function is continuous in that interval. A function f is said to be continuous from the left at a if lim f ( x) = f ( a). x в†’ a в€’ A function f is said to be continuous on an interval if it is continuous at each and every point in the interval. Continuity at an endpoint, if one exists, means f is continuous from the right (for the left endpoint) or continuous
Probability Density Functions De nition Let X be a continuous rv. Then a probability distribution or probability density function (pdf) of X is a function f(x) such that for any two numbers a and b with a b, P(a X b) = Z b a f(x)dx That is, the probability that X takes on a value in the interval [a;b] is the The study of continuous functions is a case in point - by requiring a function to be continuous, we obtain enough information to deduce powerful theorems, such as the In-termediate Value Theorem. However, the de nition of continuity is exible enough that there are a wide, and interesting, variety of continuous functions. Indeed, many func-
Piecewise Continuous Functions Dartmouth College

Continuous Functions. Section 4.2 Discrete and Continuous Domains 155 Work with a partner. Write a function to represent each problem. Graph each function. Describe the domain and range of each function. Is the domain discrete or continuous? 2 ACTIVITY: Discrete and Continuous Domains a. You are in charge of reserving, The function f(x) = x2 is continuous at x = 0 by this definition. It is also continuous at every other point on the real line by this definition. If a function is continuous at every point in its domain, we call it a continuous function. The following functions are all continuous: 1 †.
Continuity of Functions UserPages

(PDF) Strong Insertion of a Contra-$alpha$-continuous. The function f(x) = x2 is continuous at x = 0 by this definition. It is also continuous at every other point on the real line by this definition. If a function is continuous at every point in its domain, we call it a continuous function. The following functions are all continuous: 1 †https://zh.wikipedia.org/zh-hant/Talk:%E8%BF%9E%E7%BB%AD%E5%87%BD%E6%95%B0 ©x H2M071H3q qKYuXt2aA yShoOf8t ywmairhe n 0LwL3CH.O T lA ZlVl s 3rgi sg KhptIsX or 8eYs ie 7r CvDeed u.4 x 3M HaRdvex 3w qiCtah8 HIbn Mf8ilnui dt fe ….

Continuous Functions Q What does it mean for a function to be continuous at a point? Answer- In mathematics, we have a definition that consists of three concepts that are linked in a special way. Consider the following definition. Definition- Let P=(af, (a))be a point on the curve f. We say a function f is continuous at a point P if and only if the following relationship is satisfied. Probability Distributions for Continuous Variables Definition Let X be a continuous r.v. Then a probability distribution or probability density function (pdf) of X is a function f (x) such that for any two numbers a and b with a ≤ b, we have The probability that X is in the interval [a, b] can be calculated by integrating the pdf …
This function is also discontinuous. Taking into consideration all the information gathered from the examples of continuous and discontinuous functions shown above, we define a continuous functions as follows: Function f is continuous at a point a if the following conditions are satisfied. Section 4.2 Discrete and Continuous Domains 155 Work with a partner. Write a function to represent each problem. Graph each function. Describe the domain and range of each function. Is the domain discrete or continuous? 2 ACTIVITY: Discrete and Continuous Domains a. You are in charge of reserving
Lecture 17 - Piecewise continuous functions and improper integrals In this lecture, we will review piecewise continuous functions and improper integrals. We will need both of these notions in the next topic: the Laplace Transform. Intuitively, a function is said to be continuous if its graph has no breaks; it can be sketched without without A function f is said to be continuous from the left at a if lim f ( x) = f ( a). x в†’ a в€’ A function f is said to be continuous on an interval if it is continuous at each and every point in the interval. Continuity at an endpoint, if one exists, means f is continuous from the right (for the left endpoint) or continuous
This function is also discontinuous. Taking into consideration all the information gathered from the examples of continuous and discontinuous functions shown above, we define a continuous functions as follows: Function f is continuous at a point a if the following conditions are satisfied. 3.2 Limits and Continuity of Functions of Two or More Variables. 3.2.1 Elementary Notions of Limits We wish to extend the notion of limits studied in Calculus I. Recall that when we write lim x!a f(x) = L, we mean that f can be made as close as we want to L, by taking xclose enough to …
Discrete Probability Density Function The discrete probability density function (PDF) of a discrete random variable X can be represented in a table, graph, or formula, and provides the probabilities Pr(X = x) for all possible values of x. In calculus, a continuous function is a real-valued function whose graph does not have any breaks or holes. Continuity lays the foundational groundwork for the intermediate value theorem and extreme value theorem. They are in some sense the ``nicest" functions possible, and many proofs in real analysis rely on approximating arbitrary functions by continuous functions.
26 3. Continuous Functions Example 3.17. The function f: R → R given by f(x) = x+3x3 +5x5 1+x2 +x4 is continuous on R since it is a rational function whose denominator never vanishes. In addition to forming sums, products and quotients, another way to build up ©x H2M071H3q qKYuXt2aA yShoOf8t ywmairhe n 0LwL3CH.O T lA ZlVl s 3rgi sg KhptIsX or 8eYs ie 7r CvDeed u.4 x 3M HaRdvex 3w qiCtah8 HIbn Mf8ilnui dt fe …
Continuity (exercises with detailed solutions) 1. Verify that f(x) = p x is continuous at x0 for every x0 ‚ 0. 2. Verify that f(x) = 1 x ¡ 1 x0 is continuous at x0 for every x0 6= 0. 3. Draw the graph and study the discontinuity points of f(x) = [sinx]. 4. described with a joint probability mass function. If Xand Yare continuous, this distribution can be described with a joint probability density function. Example: Plastic covers for CDs (Discrete joint pmf) Measurements for the length and width of a rectangular plastic covers for CDs are rounded to the nearest mm(so they are discrete).
sum of continuous functions is a continuous function, and that a multiple of a continuous function is a continuous function. For real-valued functions (i.e., if Y = R), we can also de ne the product fg and (if 8x2X: f(x) 6= 0) the reciprocal 1 =f of functions pointwise, and we can show that if f and gare continuous then so are fgand 1=f. 2 Determine if a function is continuous on a given interval. A variation of this question is to determine the set (that is all the values of x) on which a function is continuous. Whenever possible, try to use the theorems. But in situations where the theorems do not apply, you must use the de–nition of …
1 Probability Density Function and Cumulative Distribution Function Definition1.1(Probabilitydensityfunction). Arrvissaidtobe(absolutely) continuous if there exists a real-valued function f X such that, for any subset B⊂R: P(X∈B) = Z B f X(x)dx (1) Thenf X iscalledtheprobability density function (pdf)oftherandomvari-ableX. Ticket out the Door – Discrete vs. Continuous You are traveling over winter break on a plane from Austin Intercontinental Airport (AUS) to Los Angeles, California (LAX), describe 3 discrete and 3 continuous data examples you might encounter during your trip: Discrete Examples Continuous Examples 1. 1. 2. 2. 3. 3.
The objective of the paper is to introduce a new types of continuous maps and irresolute functions called О”*-locally continuous functions and О”*-irresolute maps in topological spaces. Such a curve is denoted f(x) and is called a (continuous) probability density function. Now, you might recall that a density histogram is defined so that the area of each rectangle equals the relative frequency of the corresponding class, and the area of the entire histogram equals 1.

C. CONTINUITY AND DISCONTINUITY 3 We say a function is continuous if its domain is an interval, and it is continuous at every point of that interval. A point of discontinuity is always understood to be isolated, i.e., it is the only bad point for the function on some interval. We illustrate the point of these definitions. Ticket out the Door – Discrete vs. Continuous You are traveling over winter break on a plane from Austin Intercontinental Airport (AUS) to Los Angeles, California (LAX), describe 3 discrete and 3 continuous data examples you might encounter during your trip: Discrete Examples Continuous Examples 1. 1. 2. 2. 3. 3.