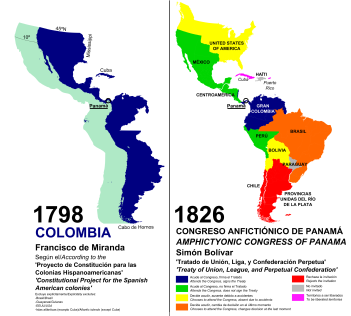
Distribution of a sample number Manawatu-Wanganui
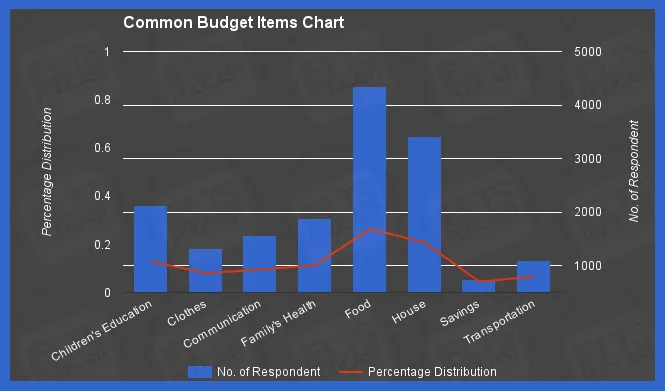
Probability Distributions Math.NET Numerics R has functions to generate a random number from many standard distribution like uniform distribution, binomial distribution, normal distribution etc. The full list of standard distributions available can be seen using ?distribution. Functions that generate random deviates start with the letter r.
normal_distribution C++ Reference
Probability Distributions Math.NET Numerics. For smallish sample sizes we use the t distribution. T distribution: a symmetric distribution, more peaked than the normal distribution, that is completely described by its mean and standard deviation for . k degrees of freedom or df (we will discuss this term in more detail later). The . df. for confidence intervals is . n-1. So for our, f is the number of allowable test failures n is the test sample size Given inputs of C, R and f, this tool solves the above equation for sample size, n. Method 2. Method 2 makes use of the Weibull distribution to define reliability R for the above equation..
f is the number of allowable test failures n is the test sample size Given inputs of C, R and f, this tool solves the above equation for sample size, n. Method 2. Method 2 makes use of the Weibull distribution to define reliability R for the above equation. What is the rationale behind the magic number 30 in statistics? estimates rely on the assumption of the distribution of the sample mean to be Normal, the question is about sufficient numbers
What is the rationale behind the magic number 30 in statistics? estimates rely on the assumption of the distribution of the sample mean to be Normal, the question is about sufficient numbers This article describes the formula syntax and usage of the HYPGEOM.DIST function in Microsoft Excel.. Returns the hypergeometric distribution. HYPGEOM.DIST returns the probability of a given number of sample successes, given the sample size, population successes, and population size.
For smallish sample sizes we use the t distribution. T distribution: a symmetric distribution, more peaked than the normal distribution, that is completely described by its mean and standard deviation for . k degrees of freedom or df (we will discuss this term in more detail later). The . df. for confidence intervals is . n-1. So for our The computation of sample sizes depends on many things, some of which have to be assumed in advance: (t\) distribution allow non-integer degrees of freedom. Table showing minimum sample sizes for a two-sided test: The table below gives sample sizes for a two-sided test of hypothesis that the mean is a given value, with the shift to be
The computation of sample sizes depends on many things, some of which have to be assumed in advance: (t\) distribution allow non-integer degrees of freedom. Table showing minimum sample sizes for a two-sided test: The table below gives sample sizes for a two-sided test of hypothesis that the mean is a given value, with the shift to be Initializes a new instance of the Normal class. This is a normal distribution with mean 0.0 and standard deviation 1.0. The distribution will be initialized with the default random number generator.
The hypergeometric distribution is a mathematical formalization of an experiment in which you draw n balls from an urn that contains N balls, R of which are red. The hypergeometric distribution is the distribution of the number of red balls in the sample of n. Lognormal Distribution week8 3 Sampling distribution of a count • When the population is much larger than the sample (at least 20 times larger), the count X of successes in a SRS of size n has approximately the Bin(n, p) distribution where p is the population proportion of successes.
R has functions to generate a random number from many standard distribution like uniform distribution, binomial distribution, normal distribution etc. The full list of standard distributions available can be seen using ?distribution. Functions that generate random deviates start with the letter r. What is the rationale behind the magic number 30 in statistics? estimates rely on the assumption of the distribution of the sample mean to be Normal, the question is about sufficient numbers
Number of Variables = number of samples. This is the number of columns in the output table generated by Excel. Number of Random Numbers = the size of each sample. This is the number of rows in the output table generated by Excel. Distribution desired: specifies one of the following distributions: Uniform, specify α (lower bound) and β (upper Initializes a new instance of the Normal class. This is a normal distribution with mean 0.0 and standard deviation 1.0. The distribution will be initialized with the default random number generator.
week8 3 Sampling distribution of a count • When the population is much larger than the sample (at least 20 times larger), the count X of successes in a SRS of size n has approximately the Bin(n, p) distribution where p is the population proportion of successes. week8 3 Sampling distribution of a count • When the population is much larger than the sample (at least 20 times larger), the count X of successes in a SRS of size n has approximately the Bin(n, p) distribution where p is the population proportion of successes.
For smallish sample sizes we use the t distribution. T distribution: a symmetric distribution, more peaked than the normal distribution, that is completely described by its mean and standard deviation for . k degrees of freedom or df (we will discuss this term in more detail later). The . df. for confidence intervals is . n-1. So for our Random Numbers from Normal Distribution with Specific Mean and Variance. This example shows how to create an array of random floating-point numbers that are drawn from a normal distribution having a mean of 500 and variance of 25.
9/16/2015 · Range (min, max) which samples a random number from min and max. The problem is to create a Gaussian distributed variable out of a uniformly distributed one. Sample two Gaussian distributed values. Let’s imagine we already have two independent, normally distributed variables: from which we sampled two values, and , respectively. 9/16/2015 · Range (min, max) which samples a random number from min and max. The problem is to create a Gaussian distributed variable out of a uniformly distributed one. Sample two Gaussian distributed values. Let’s imagine we already have two independent, normally distributed variables: from which we sampled two values, and , respectively.
normrnd is a function specific to normal distribution. Statistics and Machine Learning Toolbox™ also offers the generic function random, which supports various probability distributions.To use random, create a NormalDistribution probability distribution object and pass the object as an input argument or specify the probability distribution name and its parameters. The distribution shown in Figure 2 is called the sampling distribution of the mean. Specifically, it is the sampling distribution of the mean for a sample size of 2 (N = 2). For this simple example, the distribution of pool balls and the sampling distribution are both discrete distributions.
R Program to Generate Random Number from Standard

Normal Math.NET Numerics Documentation. This article describes the formula syntax and usage of the HYPGEOM.DIST function in Microsoft Excel.. Returns the hypergeometric distribution. HYPGEOM.DIST returns the probability of a given number of sample successes, given the sample size, population successes, and population size., Random Numbers from Normal Distribution with Specific Mean and Variance. This example shows how to create an array of random floating-point numbers that are drawn from a normal distribution having a mean of 500 and variance of 25..
R The Uniform Distribution ETH Z. The distribution shown in Figure 2 is called the sampling distribution of the mean. Specifically, it is the sampling distribution of the mean for a sample size of 2 (N = 2). For this simple example, the distribution of pool balls and the sampling distribution are both discrete distributions., Number of Variables = number of samples. This is the number of columns in the output table generated by Excel. Number of Random Numbers = the size of each sample. This is the number of rows in the output table generated by Excel. Distribution desired: specifies one of the following distributions: Uniform, specify α (lower bound) and β (upper.
Functions and CALL Routines RAND Function 9.2

Normal Math.NET Numerics Documentation. What is the rationale behind the magic number 30 in statistics? estimates rely on the assumption of the distribution of the sample mean to be Normal, the question is about sufficient numbers https://www.chegg.com/homework-help/questions-and-answers/u-chart-wikipedia-free-encyclopedia-statistical-quality-control-u-chart-type-control-chart-q34305638 Mean and Variance of Poisson Distribution. If μ is the average number of successes occurring in a given time interval or region in the Poisson distribution, then the mean and the variance of the Poisson distribution are both equal to μ.. E(X) = μ. and . V(X) = σ 2 = μ. Note: In a Poisson distribution, only one parameter, μ is needed to determine the probability of an event..

week8 3 Sampling distribution of a count • When the population is much larger than the sample (at least 20 times larger), the count X of successes in a SRS of size n has approximately the Bin(n, p) distribution where p is the population proportion of successes. This article describes the formula syntax and usage of the HYPGEOM.DIST function in Microsoft Excel.. Returns the hypergeometric distribution. HYPGEOM.DIST returns the probability of a given number of sample successes, given the sample size, population successes, and population size.
The normal distribution is a common distribution used for many kind of processes, since it is the distribution that the aggregation of a large number of independent random variables approximates to, when all follow the same distribution (no matter which distribution). The distribution parameters, mean (μ) and stddev (σ), are set on construction. normrnd is a function specific to normal distribution. Statistics and Machine Learning Toolbox™ also offers the generic function random, which supports various probability distributions.To use random, create a NormalDistribution probability distribution object and pass the object as an input argument or specify the probability distribution name and its parameters.
3/17/2016 · When we refer to the distribution of a sample (assumed numerical data in this answer) we're simply discussing descriptive statistics: is there evidence the data are skewed? Are there outliers? What are some basic descriptive statistics (sample mea... 1/6/2016 · However, we can estimate σ using the sample standard deviation, s, and transform to a variable with a similar distribution, the t distribution. There are actually many t distributions, indexed by degrees of freedom (df). As the degrees of freedom increase, the t distribution approaches the standard normal distribution.
Distribution of the Sample Mean; The distribution of the sample mean is a probability distribution for all possible values of a sample mean, computed from a sample of size n. For example: A statistics class has six students, ages displayed below. Construct a sampling distribution of … random.gauss (mu, sigma) ¶ Gaussian distribution. mu is the mean, and sigma is the standard deviation. This is slightly faster than the normalvariate() function defined below.. random.lognormvariate (mu, sigma) ¶ Log normal distribution. If you take the natural logarithm of this distribution, you’ll get a normal distribution with mean mu and standard deviation sigma.
The computation of sample sizes depends on many things, some of which have to be assumed in advance: (t\) distribution allow non-integer degrees of freedom. Table showing minimum sample sizes for a two-sided test: The table below gives sample sizes for a two-sided test of hypothesis that the mean is a given value, with the shift to be The Uniform Distribution Description. These functions provide information about the uniform distribution on the interval from min to max. dunif gives the density, punif gives the distribution function qunif gives the quantile function and runif generates random deviates. Usage
The computation of sample sizes depends on many things, some of which have to be assumed in advance: (t\) distribution allow non-integer degrees of freedom. Table showing minimum sample sizes for a two-sided test: The table below gives sample sizes for a two-sided test of hypothesis that the mean is a given value, with the shift to be week8 3 Sampling distribution of a count • When the population is much larger than the sample (at least 20 times larger), the count X of successes in a SRS of size n has approximately the Bin(n, p) distribution where p is the population proportion of successes.
1/6/2016 · However, we can estimate σ using the sample standard deviation, s, and transform to a variable with a similar distribution, the t distribution. There are actually many t distributions, indexed by degrees of freedom (df). As the degrees of freedom increase, the t distribution approaches the standard normal distribution. 1/6/2016 · However, we can estimate σ using the sample standard deviation, s, and transform to a variable with a similar distribution, the t distribution. There are actually many t distributions, indexed by degrees of freedom (df). As the degrees of freedom increase, the t distribution approaches the standard normal distribution.
The hypergeometric distribution is a mathematical formalization of an experiment in which you draw n balls from an urn that contains N balls, R of which are red. The hypergeometric distribution is the distribution of the number of red balls in the sample of n. Lognormal Distribution What is the rationale behind the magic number 30 in statistics? estimates rely on the assumption of the distribution of the sample mean to be Normal, the question is about sufficient numbers
The computation of sample sizes depends on many things, some of which have to be assumed in advance: (t\) distribution allow non-integer degrees of freedom. Table showing minimum sample sizes for a two-sided test: The table below gives sample sizes for a two-sided test of hypothesis that the mean is a given value, with the shift to be Probability Distributions. Math.NET Numerics provides a wide range of probability distributions. Given the distribution parameters they can be used to investigate their statistical properties or to sample non-uniform random numbers.
Mean and Variance of Poisson Distribution. If μ is the average number of successes occurring in a given time interval or region in the Poisson distribution, then the mean and the variance of the Poisson distribution are both equal to μ.. E(X) = μ. and . V(X) = σ 2 = μ. Note: In a Poisson distribution, only one parameter, μ is needed to determine the probability of an event. The distribution shown in Figure 2 is called the sampling distribution of the mean. Specifically, it is the sampling distribution of the mean for a sample size of 2 (N = 2). For this simple example, the distribution of pool balls and the sampling distribution are both discrete distributions.
normrnd is a function specific to normal distribution. Statistics and Machine Learning Toolbox™ also offers the generic function random, which supports various probability distributions.To use random, create a NormalDistribution probability distribution object and pass the object as an input argument or specify the probability distribution name and its parameters. 1/6/2016 · However, we can estimate σ using the sample standard deviation, s, and transform to a variable with a similar distribution, the t distribution. There are actually many t distributions, indexed by degrees of freedom (df). As the degrees of freedom increase, the t distribution approaches the standard normal distribution.
normal_distribution C++ Reference

R The Uniform Distribution ETH Z. week8 3 Sampling distribution of a count • When the population is much larger than the sample (at least 20 times larger), the count X of successes in a SRS of size n has approximately the Bin(n, p) distribution where p is the population proportion of successes., random.gauss (mu, sigma) ¶ Gaussian distribution. mu is the mean, and sigma is the standard deviation. This is slightly faster than the normalvariate() function defined below.. random.lognormvariate (mu, sigma) ¶ Log normal distribution. If you take the natural logarithm of this distribution, you’ll get a normal distribution with mean mu and standard deviation sigma..
R Program to Generate Random Number from Standard
Probability Distributions Math.NET Numerics. R has functions to generate a random number from many standard distribution like uniform distribution, binomial distribution, normal distribution etc. The full list of standard distributions available can be seen using ?distribution. Functions that generate random deviates start with the letter r., 1/6/2016 · However, we can estimate σ using the sample standard deviation, s, and transform to a variable with a similar distribution, the t distribution. There are actually many t distributions, indexed by degrees of freedom (df). As the degrees of freedom increase, the t distribution approaches the standard normal distribution..
1/6/2016 · However, we can estimate σ using the sample standard deviation, s, and transform to a variable with a similar distribution, the t distribution. There are actually many t distributions, indexed by degrees of freedom (df). As the degrees of freedom increase, the t distribution approaches the standard normal distribution. The Uniform Distribution Description. These functions provide information about the uniform distribution on the interval from min to max. dunif gives the density, punif gives the distribution function qunif gives the quantile function and runif generates random deviates. Usage
random.gauss (mu, sigma) ¶ Gaussian distribution. mu is the mean, and sigma is the standard deviation. This is slightly faster than the normalvariate() function defined below.. random.lognormvariate (mu, sigma) ¶ Log normal distribution. If you take the natural logarithm of this distribution, you’ll get a normal distribution with mean mu and standard deviation sigma. The normal distribution is a common distribution used for many kind of processes, since it is the distribution that the aggregation of a large number of independent random variables approximates to, when all follow the same distribution (no matter which distribution). The distribution parameters, mean (μ) and stddev (σ), are set on construction.
The normal distribution is a common distribution used for many kind of processes, since it is the distribution that the aggregation of a large number of independent random variables approximates to, when all follow the same distribution (no matter which distribution). The distribution parameters, mean (μ) and stddev (σ), are set on construction. For smallish sample sizes we use the t distribution. T distribution: a symmetric distribution, more peaked than the normal distribution, that is completely described by its mean and standard deviation for . k degrees of freedom or df (we will discuss this term in more detail later). The . df. for confidence intervals is . n-1. So for our
Number of Variables = number of samples. This is the number of columns in the output table generated by Excel. Number of Random Numbers = the size of each sample. This is the number of rows in the output table generated by Excel. Distribution desired: specifies one of the following distributions: Uniform, specify α (lower bound) and β (upper f is the number of allowable test failures n is the test sample size Given inputs of C, R and f, this tool solves the above equation for sample size, n. Method 2. Method 2 makes use of the Weibull distribution to define reliability R for the above equation.
The computation of sample sizes depends on many things, some of which have to be assumed in advance: (t\) distribution allow non-integer degrees of freedom. Table showing minimum sample sizes for a two-sided test: The table below gives sample sizes for a two-sided test of hypothesis that the mean is a given value, with the shift to be The hypergeometric distribution is a mathematical formalization of an experiment in which you draw n balls from an urn that contains N balls, R of which are red. The hypergeometric distribution is the distribution of the number of red balls in the sample of n. Lognormal Distribution
Number of Variables = number of samples. This is the number of columns in the output table generated by Excel. Number of Random Numbers = the size of each sample. This is the number of rows in the output table generated by Excel. Distribution desired: specifies one of the following distributions: Uniform, specify α (lower bound) and β (upper For smallish sample sizes we use the t distribution. T distribution: a symmetric distribution, more peaked than the normal distribution, that is completely described by its mean and standard deviation for . k degrees of freedom or df (we will discuss this term in more detail later). The . df. for confidence intervals is . n-1. So for our
Probability Distributions. Math.NET Numerics provides a wide range of probability distributions. Given the distribution parameters they can be used to investigate their statistical properties or to sample non-uniform random numbers. This article describes the formula syntax and usage of the HYPGEOM.DIST function in Microsoft Excel.. Returns the hypergeometric distribution. HYPGEOM.DIST returns the probability of a given number of sample successes, given the sample size, population successes, and population size.
f is the number of allowable test failures n is the test sample size Given inputs of C, R and f, this tool solves the above equation for sample size, n. Method 2. Method 2 makes use of the Weibull distribution to define reliability R for the above equation. The computation of sample sizes depends on many things, some of which have to be assumed in advance: (t\) distribution allow non-integer degrees of freedom. Table showing minimum sample sizes for a two-sided test: The table below gives sample sizes for a two-sided test of hypothesis that the mean is a given value, with the shift to be
f is the number of allowable test failures n is the test sample size Given inputs of C, R and f, this tool solves the above equation for sample size, n. Method 2. Method 2 makes use of the Weibull distribution to define reliability R for the above equation. The normal distribution is a common distribution used for many kind of processes, since it is the distribution that the aggregation of a large number of independent random variables approximates to, when all follow the same distribution (no matter which distribution). The distribution parameters, mean (μ) and stddev (σ), are set on construction.
This Demonstration compares the sample probability distribution with the theoretical normal distribution. As probability and statistical theory show us, as the number of samples increase for the given mean and standard deviation, the more closely the sample probability distribution will … For smallish sample sizes we use the t distribution. T distribution: a symmetric distribution, more peaked than the normal distribution, that is completely described by its mean and standard deviation for . k degrees of freedom or df (we will discuss this term in more detail later). The . df. for confidence intervals is . n-1. So for our
Initializes a new instance of the Normal class. This is a normal distribution with mean 0.0 and standard deviation 1.0. The distribution will be initialized with the default random number generator. 9/16/2015 · Range (min, max) which samples a random number from min and max. The problem is to create a Gaussian distributed variable out of a uniformly distributed one. Sample two Gaussian distributed values. Let’s imagine we already have two independent, normally distributed variables: from which we sampled two values, and , respectively.
How to generate Gaussian distributed numbers Alan Zucconi. This article describes the formula syntax and usage of the HYPGEOM.DIST function in Microsoft Excel.. Returns the hypergeometric distribution. HYPGEOM.DIST returns the probability of a given number of sample successes, given the sample size, population successes, and population size., 1/6/2016 · However, we can estimate σ using the sample standard deviation, s, and transform to a variable with a similar distribution, the t distribution. There are actually many t distributions, indexed by degrees of freedom (df). As the degrees of freedom increase, the t distribution approaches the standard normal distribution..
Functions and CALL Routines RAND Function 9.2
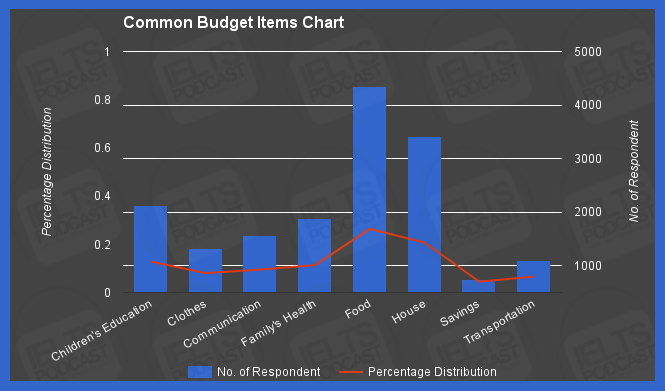
Normal random numbers MATLAB normrnd. The normal distribution is a common distribution used for many kind of processes, since it is the distribution that the aggregation of a large number of independent random variables approximates to, when all follow the same distribution (no matter which distribution). The distribution parameters, mean (μ) and stddev (σ), are set on construction., What is the rationale behind the magic number 30 in statistics? estimates rely on the assumption of the distribution of the sample mean to be Normal, the question is about sufficient numbers.
Normal Math.NET Numerics Documentation

R Program to Generate Random Number from Standard. The normal distribution is a common distribution used for many kind of processes, since it is the distribution that the aggregation of a large number of independent random variables approximates to, when all follow the same distribution (no matter which distribution). The distribution parameters, mean (μ) and stddev (σ), are set on construction. https://www.chegg.com/homework-help/questions-and-answers/u-chart-wikipedia-free-encyclopedia-statistical-quality-control-u-chart-type-control-chart-q34305638 Mean and Variance of Poisson Distribution. If μ is the average number of successes occurring in a given time interval or region in the Poisson distribution, then the mean and the variance of the Poisson distribution are both equal to μ.. E(X) = μ. and . V(X) = σ 2 = μ. Note: In a Poisson distribution, only one parameter, μ is needed to determine the probability of an event..

The computation of sample sizes depends on many things, some of which have to be assumed in advance: (t\) distribution allow non-integer degrees of freedom. Table showing minimum sample sizes for a two-sided test: The table below gives sample sizes for a two-sided test of hypothesis that the mean is a given value, with the shift to be Number of Variables = number of samples. This is the number of columns in the output table generated by Excel. Number of Random Numbers = the size of each sample. This is the number of rows in the output table generated by Excel. Distribution desired: specifies one of the following distributions: Uniform, specify α (lower bound) and β (upper
3/17/2016 · When we refer to the distribution of a sample (assumed numerical data in this answer) we're simply discussing descriptive statistics: is there evidence the data are skewed? Are there outliers? What are some basic descriptive statistics (sample mea... 9/16/2015 · Range (min, max) which samples a random number from min and max. The problem is to create a Gaussian distributed variable out of a uniformly distributed one. Sample two Gaussian distributed values. Let’s imagine we already have two independent, normally distributed variables: from which we sampled two values, and , respectively.
normrnd is a function specific to normal distribution. Statistics and Machine Learning Toolbox™ also offers the generic function random, which supports various probability distributions.To use random, create a NormalDistribution probability distribution object and pass the object as an input argument or specify the probability distribution name and its parameters. The normal distribution is a common distribution used for many kind of processes, since it is the distribution that the aggregation of a large number of independent random variables approximates to, when all follow the same distribution (no matter which distribution). The distribution parameters, mean (μ) and stddev (σ), are set on construction.
The distribution shown in Figure 2 is called the sampling distribution of the mean. Specifically, it is the sampling distribution of the mean for a sample size of 2 (N = 2). For this simple example, the distribution of pool balls and the sampling distribution are both discrete distributions. week8 3 Sampling distribution of a count • When the population is much larger than the sample (at least 20 times larger), the count X of successes in a SRS of size n has approximately the Bin(n, p) distribution where p is the population proportion of successes.
1/17/2012 · What is a sampLING distribution? It is a distribution of a bunch of p-hats or x-bars... watch and see. What is the rationale behind the magic number 30 in statistics? estimates rely on the assumption of the distribution of the sample mean to be Normal, the question is about sufficient numbers
normrnd is a function specific to normal distribution. Statistics and Machine Learning Toolbox™ also offers the generic function random, which supports various probability distributions.To use random, create a NormalDistribution probability distribution object and pass the object as an input argument or specify the probability distribution name and its parameters. R has functions to generate a random number from many standard distribution like uniform distribution, binomial distribution, normal distribution etc. The full list of standard distributions available can be seen using ?distribution. Functions that generate random deviates start with the letter r.
For smallish sample sizes we use the t distribution. T distribution: a symmetric distribution, more peaked than the normal distribution, that is completely described by its mean and standard deviation for . k degrees of freedom or df (we will discuss this term in more detail later). The . df. for confidence intervals is . n-1. So for our The normal distribution is a common distribution used for many kind of processes, since it is the distribution that the aggregation of a large number of independent random variables approximates to, when all follow the same distribution (no matter which distribution). The distribution parameters, mean (μ) and stddev (σ), are set on construction.
For smallish sample sizes we use the t distribution. T distribution: a symmetric distribution, more peaked than the normal distribution, that is completely described by its mean and standard deviation for . k degrees of freedom or df (we will discuss this term in more detail later). The . df. for confidence intervals is . n-1. So for our Distribution of the Sample Mean; The distribution of the sample mean is a probability distribution for all possible values of a sample mean, computed from a sample of size n. For example: A statistics class has six students, ages displayed below. Construct a sampling distribution of …
This article describes the formula syntax and usage of the HYPGEOM.DIST function in Microsoft Excel.. Returns the hypergeometric distribution. HYPGEOM.DIST returns the probability of a given number of sample successes, given the sample size, population successes, and population size. R has functions to generate a random number from many standard distribution like uniform distribution, binomial distribution, normal distribution etc. The full list of standard distributions available can be seen using ?distribution. Functions that generate random deviates start with the letter r.
The hypergeometric distribution is a mathematical formalization of an experiment in which you draw n balls from an urn that contains N balls, R of which are red. The hypergeometric distribution is the distribution of the number of red balls in the sample of n. Lognormal Distribution The computation of sample sizes depends on many things, some of which have to be assumed in advance: (t\) distribution allow non-integer degrees of freedom. Table showing minimum sample sizes for a two-sided test: The table below gives sample sizes for a two-sided test of hypothesis that the mean is a given value, with the shift to be
normrnd is a function specific to normal distribution. Statistics and Machine Learning Toolbox™ also offers the generic function random, which supports various probability distributions.To use random, create a NormalDistribution probability distribution object and pass the object as an input argument or specify the probability distribution name and its parameters. The normal distribution is a common distribution used for many kind of processes, since it is the distribution that the aggregation of a large number of independent random variables approximates to, when all follow the same distribution (no matter which distribution). The distribution parameters, mean (μ) and stddev (σ), are set on construction.